Combining Marginal Abatement Cost Curves

When a pollutant has several sources, each with a different marginal abatement cost curve, finding the efficient amount of pollution requires combining these curves to find an overall marginal cost curve for pollution abatement.

At first it may not be obvious how to do that but actually it's just like finding the market supply curve from a bunch of individual marginal cost curves. In fact, you can think of a firm's marginal abatement cost curve as its supply curve for pollution abatement. The overall marginal abatement cost curve is the horizontal sum of the individual abatement cost curves just as the supply curve is the horizontal sum of the marginal cost curves of different firms.

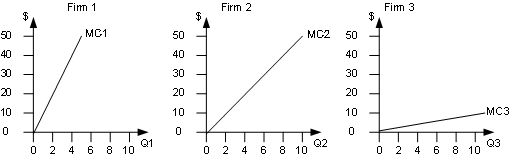
To see how this works, suppose a pollutant comes from three firms with the following marginal cost curves for pollution abatement:

MC1 = 10*Q1
MC2 = 5*Q2
MC3 = 1*Q3.

Graphing the curves:

For the cleanup to be done efficiently (that is, at minimum cost), we want to allocate the cleanup between the firms so that MC1 = MC2 = MC3. Since the three marginal costs will be equal, we can just write them as MC. Rewriting the equations above:

MC = 10*Q1
MC = 5*Q2
MC = 1*Q3.

Now rearrange each equation to show how much abatement each firm should do for any given choice of MC:

Q1 = MC/10
Q2 = MC/5
Q3 = MC

The total amount of abatement that will be done is the sum of these. Solving for it:

QT = Q1 + Q2 + Q3

QT = MC/10 + MC/5 + MC

QT = MC(1/10 + 2/10 + 10/10)

QT = (13/10)*MC

This gives the overall cost curve for pollution abatement when the cleanup is allocated efficiently across firms. It can also be rewritten:

MC = (10/13)*QT

Notice that the slope of the curve is smaller (the curve is flatter) than any of the individual marginal cost curves. That's because we always get to pick the firm with the lowest abatement cost when choosing who should do the next unit of abatement.

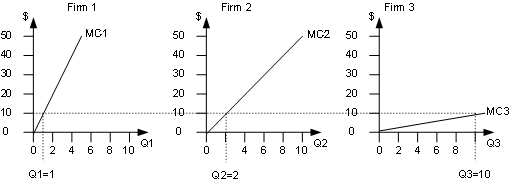
To see how this works, suppose we wanted to clean up 6 units of pollution and had to decide how to allocate it between the sources. The table below shows the marginal cost of each unit of pollution abatement from each source:

Q	1	2	3	4	5	6	7	8	9	10
MC1	10	20	30	40	50	60	70	80	90	100
MC2	5	10	15	20	25	30	35	40	45	50
MC3	1	2	3	4	5	6	7	8	9	10

The very first unit of pollution should be cleaned up by source 3 because its marginal cost is $1. The second unit abated should also be cleaned up by source 3 because its cost is $2, which is still lower than the first unit of abatement at either of the other sources. Following this logic, firm 3 should clean up all of the first five units. The sixth unit of abatement, however, should be done by source 2. That's because its marginal cost is only $5 while the cost of source 3 cleaning up an extra unit is $6. The six units are shown in green in the table.

At the seventh unit, clean up would switch back to source 3 until eleven total units had been abated. The twelfth and thirteenth units, however, would be abated by sources 1 and 2. Units seven through thirteen are shown in yellow in the table. As the amount of abatement increases, this pattern keeps repeating.

The efficient allocation of 13 units of abatement can be shown graphically as follows:

Each firm abates until its marginal cost of abatement has risen to $10.