Taxes and Permits Under Uncertainty

When the marginal benefits (MBa) and marginal costs (MCa) of pollution abatement are known with certainty, the efficient amount of pollution abatement can be achieved by either an emissions tax or a tradable permit policy. In terms of efficiency alone, the two policies are equivalent. (They have quite different distributional effects, however.) With a tax policy we set the tax to the efficient MCa and then firms will choose to clean up exactly the efficient amount. Under a permit policy we choose the amount of abatement and then firms trade permits among themselves until they have minimized the cost of achieving it. Either way we get the efficient amount of pollution at the minimum cost.

Things become more complicated when the marginal costs of abatement are not known for certain when the policy is being formulated. In that case, the policy will have to be set up based on an estimate of marginal abatement costs. If the estimate turns out to be wrong, and we aren't able to change the policy to reflect the new information, we could end up with either too much or too little abatement.

In terms of algebra, the policy would be designed to achieve the quantity of abatement (Qa) that makes the following equation hold:

MBa(Qa) = estimated MCa(Qa)

After the true marginal costs are known, efficiency would require that we clean up until the following is true:

MBa(Qa) = true MCa(Qa)

The problem is that if the estimated MCa does not equal the true MCa, the Qa from the second equation will be different from the Qa in the first equation. If we can't change the policy, however, we won't necessarily be able to get to efficiency.

In this situation, taxes and permits are no longer equivalent. In some circumstances it will be much better to use a tax while in others it will be much better to use permits. Which policy is better depends on the steepness of the MCa and MBa curves. To see how this works, consider two extreme examples.

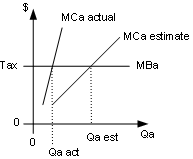
First, suppose the MBa curve is horizontal (the marginal benefit of abatement is constant). In this case it is most efficient to use an emissions tax. If we set the tax to the value of MBa, we'll get the efficient amount of clean up no matter what the MCa curve turns out to look like. Firms will always choose the level of clean up that makes MCa equal to the tax. If our estimate of the MCa curve was wrong, we'll get more or less abatement than we expected, but it will be the efficient amount. The graph below shows what would happen if the MCa curve was steeper than expected:

Less abatement would be done than expected.

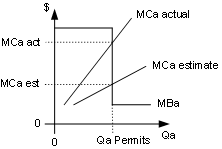
Now suppose the MBa curve starts out horizontal at a high value and then drops abruptly to zero once a critical level of abatement has been reached (it looks like a step down). This would happen for a threshold pollutant which causes damage when present at high concentrations but causes no damage at low concentrations. Efficiency would almost always require that we clean up to the critical level. (The only time we wouldn't want to is when the marginal cost of abatement is very, very high.) A tax policy would not work well because it would guarantee the MCa but would allow the quantity of abatement to adjust once the actual marginal cost curve becomes known. A permit policy, however, would be just the right thing: it would guarantee the level of abatement and MCa would adjust. In other words, if our estimate of the MCa curve was wrong, we'll still get the efficient level of abatement but it might be at a higher or lower marginal cost than we expected. This case is illustrated below:

The permit policy guarantees the amount of abatement but the marginal cost of the last unit abated will be higher than expected.

Additional Information